Introduction
Computing square root is a critical concept in mathematics and within this programming language one is able to embark on this basic computation in a very simple and efficient manner. Whether you’re involved in an experiment, simulations, data analysis or using machine learning, calculating square roots in Python is crucial. In this guide, you will learn various ways of approximating square root in Python; whether it is by use of inbuilt functions or by using other developed python libraries which are efficient in solving mathematics computation.

Learning Outcomes
- Understand what a square root is and its significance in programming.
- Learn how to compute square roots using Python’s built-in
mathmodule. - Discover alternative ways to find square roots using external libraries like
numpy. - Be able to handle edge cases such as negative numbers.
- Implement square root calculations in real-world examples.
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if y is the square root of x, then:
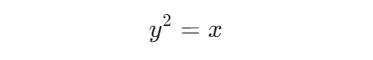
This means 𝑦 × 𝑦 = 𝑥. For example, the square root of 9 is 3 because 3 × 3 = 9.
Notation:
The square root of a number xxx is commonly denoted as:
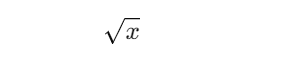
Why It’s Important to Understand Square Roots
Square roots are essential across mathematics, sciences, and technical professions because they ground understanding of these operations. Whether you are just doing addition and subtraction, or solving equations that involve difficult algorithms, the understanding of how square roots work can enable you solve many problems effectively. Below are several key reasons why understanding square roots is important:
- Foundation for Algebra: Square roots are essential for solving quadratic equations and understanding powers and exponents.
- Geometry and Distance: Square roots help calculate distances, areas, and diagonals, especially in geometry and architecture.
- Physics and Engineering: Key formulas in physics and engineering, like velocity and stress analysis, involve square roots.
- Financial Calculations: Used in risk analysis, standard deviation, and growth models in finance and economics.
- Data Science & Machine Learning: Square roots are vital in optimization algorithms, error measurements, and statistical functions.
- Building Problem-Solving Skills: Enhances mathematical reasoning and logic for tackling more complex problems.
Methods to Compute Square Roots in Python
Python being an open source language, there are many ways to arrive at the square root of a number depending on the situations at hand. Below are the most common methods, along with detailed descriptions:
Using the math.sqrt() Function
The simple and standard method for finding the square root of a floating number in Python uses the math.sqrt() function from the inbuilt math library.
Example:
import math
print(math.sqrt(25)) # Output: 5.0
print(math.sqrt(2)) # Output: 1.4142135623730951The math.sqrt() function only works with non-negative numbers and returns a float. If a negative number is passed, it raises a ValueError.
Using the cmath.sqrt() Function for Complex Numbers
For cases where you need to compute the square root of negative numbers, the cmath.sqrt() function from the cmath (complex math) module is used. This method returns a complex number as a result.
This method allows the computation of square roots of both positive and negative numbers. It returns a complex number (in the form of a + bj) even when the input is negative.
Example:
import cmath
print(cmath.sqrt(-16)) # Output: 4j
print(cmath.sqrt(25)) # Output: (5+0j)It is used when working with complex numbers or when negative square roots need to be calculated.
Using the Exponentiation Operator **
In Python, the exponentiation operator (**) can be used to calculate square roots by raising a number to the power of 1/2 (0.5).
This method works for both integers and floats. If the number is positive, it returns a float. If the number is negative, it raises a ValueError, as this method does not handle complex numbers.
Example:
print(16 ** 0.5) # Output: 4.0
print(2 ** 0.5) # Output: 1.4142135623730951A quick and flexible method that doesn’t require importing any modules, suitable for simple calculations.
Using Newton’s Method (Iterative Approximation)
Newton and its other name the Babylonian method is a simple algorithm to estimate the square root of a given quantity. This method is as follows and is not as straightforward as the built-in functions: However, by doing this, one gets to understand how square roots are computed in the background.
This one simply begins with some guess, usually middle value, and then iteratively refines this guess until the desired precision is attained.
Example:
def newtons_sqrt(n, precision=0.00001):
guess = n / 2.0
while abs(guess * guess - n) > precision:
guess = (guess + n / guess) / 2
return guess
print(newtons_sqrt(16)) # Output: approximately 4.0
print(newtons_sqrt(2)) # Output: approximately 1.41421356237Useful for custom precision requirements or educational purposes to demonstrate the approximation of square roots.
Using the pow() Function
Python also has a built-in pow() function, which can be used to calculate the square root by raising the number to the power of 0.5.
Example:
num = 25
result = pow(num, 0.5)
print(f'The square root of {num} is {result}')
#Output: The square root of 25 is 5.0Using numpy.sqrt() for Arrays
If you are doing operations with arrays or matrices, in the numpy library there’s the numpy.sqrt() function which is optimized for such calculations as obtaining square root of every element in the array.
One of the benefits of using this approach is that to find square root of matching element you do not recompute the whole trigonometric chain, so is suitable for big data sets.
Example:
import numpy as np
arr = np.array([4, 9, 16, 25])
print(np.sqrt(arr)) # Output: [2. 3. 4. 5.]Ideal for scientific computing, data analysis, and machine learning tasks where operations on large arrays or matrices are common.
Comparison of Methods
Below is the table of comparing the methods of python square root methods:
| Method | Handles Negative Numbers | Handles Complex Numbers | Ideal for Arrays | Customizable Precision |
|---|---|---|---|---|
math.sqrt() |
No | No | No | No |
cmath.sqrt() |
Yes | Yes | No | No |
Exponentiation (**) |
No | No | No | No |
| Newton’s Method | No (without complex handling) | No (without complex handling) | No | Yes (with custom implementation) |
numpy.sqrt() |
No | Yes | Yes | No |
Real-World Use Cases for Square Roots
- In Data Science: Explain how square roots are used to calculate standard deviation, variance, and root mean square errors in machine learning models.
import numpy as np
data = [2, 4, 4, 4, 5, 5, 7, 9]
standard_deviation = np.std(data)
print(f"Standard Deviation: {standard_deviation}")- In Graphics & Animation: Square roots are commonly used in computing distances between points (Euclidean distance) in 2D or 3D spaces.
point1 = (1, 2)
point2 = (4, 6)
distance = math.sqrt((point2[0] - point1[0])**2 + (point2[1] - point1[1])**2)
print(f"Distance: {distance}") # Output: 5.0- Visualization: We can use python square root for visualizing the data.
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 10, 100)
y = np.sqrt(x)
plt.plot(x, y)
plt.title("Square Root Function")
plt.xlabel("x")
plt.ylabel("sqrt(x)")
plt.show()Performance Considerations and Optimization
Add a section comparing the computational efficiency of different square root methods, especially when working with large datasets or real-time systems.
Example:
import timeit
print(timeit.timeit("math.sqrt(144)", setup="import math"))
print(timeit.timeit("144 ** 0.5"))This will highlight the pros and cons of using one method over another, especially in terms of execution speed and memory consumption.
Handling Edge Cases
Handling edge cases is crucial when working with square root calculations in Python to ensure robustness and accuracy. This section will explore how to manage special cases like negative numbers and invalid inputs effectively.
- Error Handling: Discuss how to handle exceptions when calculating square roots, such as using
try-exceptblocks to manageValueErrorfor negative numbers inmath.sqrt().
try:
result = math.sqrt(-25)
except ValueError:
print("Cannot compute the square root of a negative number using math.sqrt()")- Complex Roots: Provide more detailed examples for handling complex roots using
cmath.sqrt()and explain when such cases occur, e.g., in signal processing or electrical engineering.
Conclusion
Python offers several choices when it comes to using for square roots; the basic type is math.sqrt() while the more developed type is numpy.sqrt() for arrays. Thus, you can select the necessary method to use for a particular case. Furthermore, knowledge of how to use cmath to solve special cases like the use of negative numbers will help to make your code appreciable.
Frequently Asked Questions
A. The easiest way is to use the math.sqrt() function, which is simple and effective for most cases.
A. Yet there is a cmath.sqrt() function which takes complex number and becomes imaginary for ratio less than zero.
A. Yes, by using the numpy.sqrt() function, you can calculate the square root for each element in an array or list.
A. Passing a negative number to math.sqrt() will raise a ValueError because square roots of negative numbers are not real.
pow(x, 0.5) the same as math.sqrt(x)?
A. Yes, pow(x, 0.5) is mathematically equivalent to math.sqrt(x), and both return the same result for non-negative numbers.
My name is Ayushi Trivedi. I am a B. Tech graduate. I have 3 years of experience working as an educator and content editor. I have worked with various python libraries, like numpy, pandas, seaborn, matplotlib, scikit, imblearn, linear regression and many more. I am also an author. My first book named #turning25 has been published and is available on amazon and flipkart. Here, I am technical content editor at Analytics Vidhya. I feel proud and happy to be AVian. I have a great team to work with. I love building the bridge between the technology and the learner.
